FBIWARNING:本文一切知识点,知识框架均来自于个人对数据分析、数据挖掘、机器学习等方面的理解,推测均出自于本人的臆测,如果对数据分析感兴趣,可以参阅可汗学院的《统计学》、各大学的数据分析和机器学习课程。
基础知识
机器学习定义
机器学习在近30多年已发展为一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、计算复杂性理论等多门学科。机器学习理论主要是设计和分析一些让计算机可以自动“学习”的算法。机器学习算法是一类从数据中自动分析获得规律,并利用规律对未知数据进行预测的算法 – 维基百科
简单从实现上来说,机器学习就是使用机器学习算法来得到目标数据集的最优近似函数的过程。
监督和无监督
监督学习所得到的结果都是已知的,即结果集是可预估的。常见的监督学习算法包括回归分析和统计分类。 无监督学习所得到的结果是未知的,即结果集是不可预估的,常见的无监督学习算法有聚类。 半监督学习继承了监督学习与无监督学习,往往采用少量的数据集使用监督学习得到部分结果,再以大量的无监督学习对结果进行验证和修正。 增强学习通过观察来学习做成如何的动作。每个动作都会对环境有所影响,学习对象根据观察到的周围环境的反馈来做出判断。
数据挖掘
数据挖掘这一词语常与机器学习相混淆,实际上,数据挖掘的总体目标是从一个数据集中提取信息,并将其转换成可理解的结构,以进一步使用。出于发现数据集知识的目的,数据挖掘设计数据管理方面、数据预处理、模型与推断方面考量、兴趣度度量、复杂度的考虑,以及发现结构、可视化及在线更新等后处理。有鉴于此目标,“数据挖掘”实际上和“数据分析”这一名词在同一维度。
机器学习框架
大多数机器学习算法的基本框架都是模型(model/Representation)、代价函数(cost function)、优化算法。
以最简单的线性回归(Linear regression)来举例: 线性回归(模型)常用于有明显线性关系简单模型预测,例如流行病学、金融资产等,其算法的代价函数为最小二乘法(代价函数),即 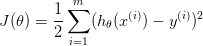 最终使用梯度下降(优化算法)得到结果。
最终使用梯度下降(优化算法)得到结果。
而在使用Logistic回归(Logistic Regression)算法时,Logistic回归(模型)使用的则是极大似然估计(代价函数),即 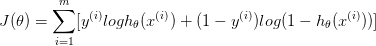 最终使用梯度下降(优化算法)得到结果。
最终使用梯度下降(优化算法)得到结果。
最小二乘和极大似然的关系
在不同的情况中使用不同的代价函数,原因是各自的响应变量y服从不同的概率分布。
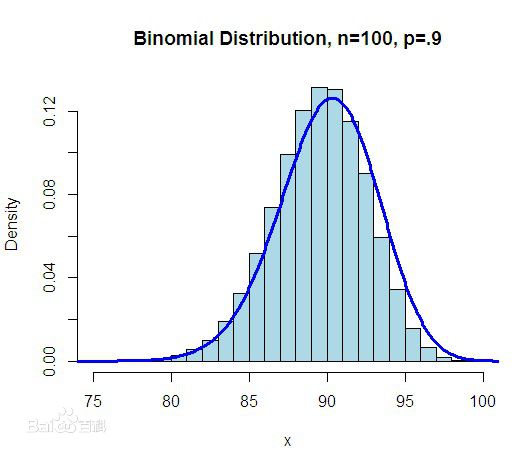
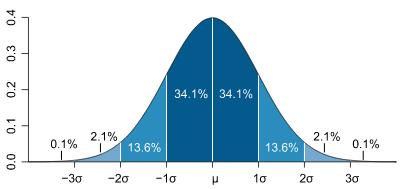
在线性回归中,前提假设是y服从正态分布,即\[y\sim N(\mu,\sigma^2)\]而Logistic回归中的y是服从二项分布的,即\[y\sim Bernoulli(\phi)\]
因而,在用极大似然估计计算时,所得到的代价函数自然是不一样的。
最小二乘是从函数形式上来看的,极大似然是从概率意义上来看的。事实上,最小二乘可以由高斯噪声假设+极大似然估计推导出来。
所以在较复杂的模型中,一个代价函数可以用不同的优化算法,不同的代价函数也可以用相同的优化算法。
代价函数
代价函数也被称作平方误差函数,有时也被称为平方误差代价函数。我们之所以要求出误差的平方和,是因为误差平方代价函数,对于大多数问题,特别是回归问题,都是一个合理的选择。
仍以线性回归作为示范,图中X为样本点,垂直蓝线是建模误差,为了得到合适的直线,我们必须令蓝线尽可能短,即建模误差最小。
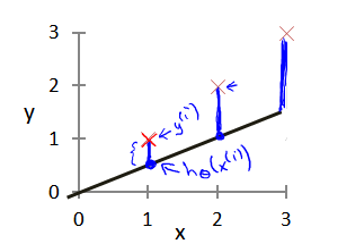
image_1b72gv22748b11ejve71o60us718.png-20.2kB
为了使代价函数最小,我们绘制套入代价函数结果的三维等高图,即可得到
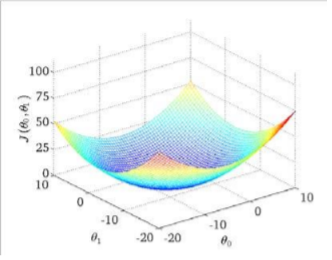
image_1b72h6eea1vc61qv74rf1t4o1t8l1l.png-69kB
图中最凹点即为代价函数最优情况。(具体函数推导详见coursera机器学习课程2-3)。
全局最优解/局部最优解
接下来,我们以梯度下降作为优化算法来计算代价函数最小值。 我们依然把一个二维数据集加入代价函数,绘制三维等高图,如图所示:
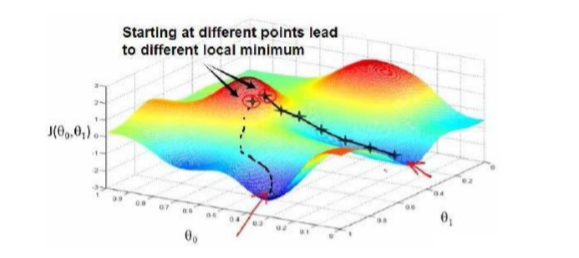
image_1b72hdcd5ehjhhk1e68rte1gsp22.png-135.5kB
无论数据初始在什么位置,我们的目标,是进入全局最优点(即全局最低点),也就是机器学习工程师们常说的下山。
想象你正在所示起点,视野范围是有限的,为了尽快下山,你会在前往目之所及选择最低的一点。当你到达之前的最低点,再以此类推继续前往最低点。 如右边的线段所示,很常见的,在下山中不断的寻找有地点,很有可能进入并停留在一个局部最低点,而非全局最优点。这种情况常发生在视距(学习率a,库中命名为alpha)的选择不合适的情况下,降低a的值虽然可以提高进入全局最优点的准确率,也会很大的降低模型的计算速度。
欠拟合和过拟合
以一个分类模型为例:
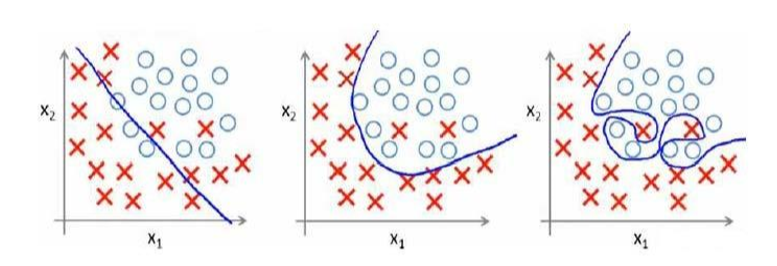
image_1b72i3cnefas1cvrjp9qp2qj22f.png-226.9kB
对一个多项式模型而言,x的次数越多,拟合效果就会越好,但是从操作上,将其控制在一个合适的范围内并不容易,图中第二个模型属于适当的分类,而第一个模型太过松散,称为欠拟合,第三个模型分类过度,称为过拟合,欠拟合和过拟合导致的调参问题一直都是机器学习使用者最大的问题。
在欠拟合中,拟合度不足,我们可以轻松的通过增加x的次数(多项式)来弥补;而在过拟合中,通常有两种处理方法:
1.使用特征工程,来抛弃一些对模型有影响却并没有实际意义的特征。 2.正则化,保留特征,但控制参数的大小。
在实际运用中,一般会同时使用这两种方法。后面会提及这两种方法的具体使用。
算法选择
主要算法
泛指被sklearn等大型库集成的算法。
1.朴素贝叶斯
朴素贝叶斯属于生成式模型(关于生成模型和判别式模型,主要还是在于是否需要求联合分布),比较简单,你只需做一堆计数即可。如果注有条件独立性假设(一个比较严格的条件),朴素贝叶斯分类器的收敛速度将快于判别模型,比如逻辑回归,所以你只需要较少的训练数据即可。即使NB条件独立假设不成立,NB分类器在实践中仍然表现的很出色。它的主要缺点是它不能学习特征间的相互作用,用mRMR中R来讲,就是特征冗余。引用一个比较经典的例子,比如,虽然你喜欢Brad Pitt和Tom Cruise的电影,但是它不能学习出你不喜欢他们在一起演的电影。
优点:
- 朴素贝叶斯模型发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率。
- 对小规模的数据表现很好,能个处理多分类任务,适合增量式训练;
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
缺点:
- 需要计算先验概率;
- 分类决策存在错误率;
- 对输入数据的表达形式很敏感。
2.Logistic Regression(逻辑回归)
逻辑回归属于判别式模型,同时伴有很多模型正则化的方法(L0, L1,L2,etc),而且你不必像在用朴素贝叶斯那样担心你的特征是否相关。与决策树、SVM相比,会得到一个不错的概率解释,你甚至可以轻松地利用新数据来更新模型(使用在线梯度下降算法-online gradient descent)。如果需要一个概率架构(比如,简单地调节分类阈值,指明不确定性,或者是要获得置信区间)。
Sigmoid函数:表达式为公式:
\[f(x)=\frac{1}{1+e^{−x}}\]
优点:
- 实现简单,广泛的应用于工业问题上;
- 分类时计算量非常小,速度很快,存储资源低;
- 便利的观测样本概率分数;
- 对逻辑回归而言,多重共线性并不是问题,它可以结合L2正则化来解决该问题;
缺点:
- 当特征空间很大时,逻辑回归的性能不是很好;
- 容易欠拟合,一般准确度不太高
- 不能很好地处理大量多类特征或变量;
- 只能处理两分类问题(在此基础上衍生出来的softmax可以用于多分类),且必须线性可分;
- 对于非线性特征,需要进行转换;
3.线性回归
线性回归是用于回归的,它不像Logistic回归那样用于分类,其基本思想是用梯度下降法对最小二乘法形式的误差函数进行优化,当然也可以用normal equation直接求得参数的解,结果为:
\[\hat{w}=(X^{T}X)^{-1}X^Ty\] 而在LWLR(局部加权线性回归)中,参数的计算表达式为:
\[\hat{w}=(X^{T}WX)^{-1}X^TWy\] 由此可见LWLR与LR不同,LWLR是一个非参数模型,因为每次进行回归计算都要遍历训练样本至少一次。
优点: + 实现简单,计算简单;
缺点: + 不能拟合非线性数据.
4.最近邻算法——KNN
KNN即最近邻算法,其主要过程为:
- 计算训练样本和测试样本中每个样本点的距离(常见的距离度量有欧式距离,马氏距离等);
- 对上面所有的距离值进行排序(升序);
- 选前k个最小距离的样本;
- 根据这k个样本的标签进行投票,得到最后的分类类别; 如何选择一个最佳的K值,这取决于数据。一般情况下,在分类时较大的K值能够减小噪声的影响,但会使类别之间的界限变得模糊。一个较好的K值可通过各种启发式技术来获取,比如,交叉验证。另外噪声和非相关性特征向量的存在会使K近邻算法的准确性减小。近邻算法具有较强的一致性结果,随着数据趋于无限,算法保证错误率不会超过贝叶斯算法错误率的两倍。对于一些好的K值,K近邻保证错误率不会超过贝叶斯理论误差率。
优点:
- 理论成熟,思想简单,既可以用来做分类也可以用来做回归;
- 可用于非线性分类;
- 训练时间复杂度为O(n);
- 对数据没有假设,准确度高,对outlier不敏感;
缺点:
- 计算量大(体现在距离计算上);
- 样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少)效果差;
- 需要大量内存;
5.决策树
决策树的一大优势就是易于解释。它可以毫无压力地处理特征间的交互关系并且是非参数化的,因此你不必担心异常值或者数据是否线性可分(举个例子,决策树能轻松处理好类别A在某个特征维度x的末端,类别B在中间,然后类别A又出现在特征维度x前端的情况)。它的缺点之一就是不支持在线学习,于是在新样本到来后,决策树需要全部重建。另一个缺点就是容易出现过拟合,但这也就是诸如随机森林RF(或提升树boosted tree)之类的集成方法的切入点。
决策树中很重要的一点就是选择一个属性进行分枝,因此要注意一下信息增益的计算公式,并深入理解它。
信息熵的计算公式如下:
\[H=-\sum^{n}_{i=1}p(x_i)log_2p(x_i)\]
其中的n代表有n个分类类别(比如假设是二类问题,那么n=2)。分别计算这2类样本在总样本中出现的概率p1和p2,这样就可以计算出未选中属性分枝前的信息熵。
现在选中一个属性x用来进行分枝,此时分枝规则是:如果x=v的话,将样本分到树的一个分支;如果不相等则进入另一个分支。很显然,分支中的样本很有可能包括2个类别,分别计算这2个分支的熵H1和H2,计算出分枝后的总信息熵H’ =p1 H1+p2 H2,则此时的信息增益ΔH = H - H’。以信息增益为原则,把所有的属性都测试一边,选择一个使增益最大的属性作为本次分枝属性。
优点:
- 计算简单,易于理解,可解释性强;
- 比较适合处理有缺失属性的样本;
- 能够处理不相关的特征;
- 在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
缺点:
- 容易发生过拟合(随机森林可以很大程度上减少过拟合);
- 忽略了数据之间的相关性;
- 对于那些各类别样本数量不一致的数据,在决策树当中,信息增益的结果偏向于那些具有更多数值的特征(只+ 要是使用了信息增益,都有这个缺点,如RF)。
5.1 Adaboosting
Adaboost是一种加和模型,每个模型都是基于上一次模型的错误率来建立的,过分关注分错的样本,而对正确分类的样本减少关注度,逐次迭代之后,可以得到一个相对较好的模型。该算法是一种典型的boosting算法,其加和理论的优势可以使用Hoeffding不等式得以解释。
优点:
- Adaboost是一种有很高精度的分类器。
- 可以使用各种方法构建子分类器,Adaboost算法提供的是框架。
- 当使用简单分类器时,计算出的结果是可以理解的,并且弱分类器的构造极其简单。
- 简单,不用做特征筛选。
- 不易发生过拟合。
缺点:
- 对离散值比较敏感
6.SVM支持向量机
支持向量机,一个经久不衰的算法,高准确率,为避免过拟合提供了很好的理论保证,而且就算数据在原特征空间线性不可分,只要给个合适的核函数,它就能运行得很好。在动辄超高维的文本分类问题中特别受欢迎。可惜内存消耗大,难以解释,运行和调参也有些烦人,而随机森林却刚好避开了这些缺点,比较实用。
优点:
- 可以解决高维问题,即大型特征空间;
- 能够处理非线性特征的相互作用;
- 无需依赖整个数据;
- 可以提高泛化能力;
缺点:
- 当观测样本很多时,效率并不是很高;
- 对非线性问题没有通用解决方案,有时候很难找到一个合适的核函数;
- 对缺失数据敏感;
- 对于核的选择也是有技巧的(libsvm中自带了四种核函数:线性核、多项式核、RBF以及sigmoid核):
第一,如果样本数量小于特征数,那么就没必要选择非线性核,简单的使用线性核就可以了; 第二,如果样本数量大于特征数目,这时可以使用非线性核,将样本映射到更高维度,一般可以得到更好的结果; 第三,如果样本数目和特征数目相等,该情况可以使用非线性核,原理和第二种一样。 对于第一种情况,也可以先对数据进行降维,然后使用非线性核,这也是一种方法。
7. 人工神经网络的优缺点
(人工神经网络目前主要是深度学习的范畴)
优点:
- 分类的准确度高;
- 并行分布处理能力强,分布存储及学习能力强,
- 对噪声神经有较强的鲁棒性和容错能力,能充分逼近复杂的非线性关系;
- 具备联想记忆的功能。
缺点:
- 神经网络需要大量的参数,如网络拓扑结构、权值和阈值的初始值;
- 不能观察之间的学习过程,输出结果难以解释,会影响到结果的可信度和可接受程度;
- 学习时间过长,甚至可能达不到学习的目的。
8、K-Means聚类
优点:
- 算法简单,容易实现 ;
- 对处理大数据集,该算法是相对可伸缩的和高效率的,因为它的复杂度大约是O(nkt),其中n是所有对象的数目,k是簇的数目,t是迭代的次数。通常k<<n。这个算法通常局部收敛。
- 算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的,且簇与簇之间区别明显时,聚类效果较好。
缺点:
- 对数据类型要求较高,适合数值型数据;
- 可能收敛到局部最小值,在大规模数据上收敛较慢
- K值比较难以选取;
- 对初值的簇心值敏感,对于不同的初始值,可能会导致不同的聚类结果;
- 不适合于发现非凸面形状的簇,或者大小差别很大的簇。
- 对于”噪声”和孤立点数据敏感,少量的该类数据能够对平均值产生极大影响。
仿生/模拟算法
通过对自然过程的模拟,对原有算法进行优化,也叫启发式算法(人工神经网络和深度学习也在其中)。 ### 9.蚁群算法 又称蚂蚁算法,是一种用来在图中寻找优化路径的机率型算法。其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。蚁群算法是一种模拟进化算法,初步的研究表明该算法具有许多优良的性质.针对PID控制器参数优化设计问题,将蚁群算法设计的结果与遗传算法设计的结果进行了比较,数值仿真结果表明,蚁群算法具有一种新的模拟进化优化方法的有效性和应用价值。
10.粒子群算法(PSO)
又称微粒群算法,该算法使用如下心理学假设:在寻求一致的认知过程中,个体往往记住自身的信念,并同时考虑同事们的信念。当其察觉同事的信念较好的时候,将进行适应性地调整。
流程如下: 初始化一群微粒(群体规模为m),包括随机的位置和速度; 评价每个微粒的适应度; 对每个微粒,将它的适应值和它经历过的最好位置pbest的作比较,如果较好,则将其作为当前的最好位置pbest; 对每个微粒,将它的适应值和全局所经历最好位置gbest的作比较,如果较好,则重新设置gbest的索引号; 根据方程(1)变化微粒的速度和位置; 如未达到结束条件(通常为足够好的适应值或达到一个预设最大代数Gmax),回到2)。
11.模拟退火算法
模拟退火算法的原理同金属退火类似:将搜寻空间内每一点想像成空气内的分子;分子的能量,就是它本身的动能;而搜寻空间内的每一点,也像空气分子一样带有“能量”,以表示该点对命题的合适程度。算法先以搜寻空间内一个任意点作起始:每一步先选择一个“邻居”,然后再计算从现有位置到达“邻居”的概率。
在一个模型中,模拟退火算法起到的作用是跳崖,防止进入局部最优解。
12.禁忌搜索算法
类似于模拟退火算法的目标,具体方式为其先创立一个初始化的方案,基于此,算法“移动”到一相邻的方案。经过许多连续的移动过程,以提高解的质量。
其它优化算法
13.TF-IDF算法
TF-IDF是一种文本统计方法,字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降。TF-IDF加权的各种形式常被搜索引擎应用,作为文件与用户查询之间相关程度的度量或评级。常见于将文本转换为数值以相互比较和计算。
算法过程: 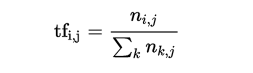
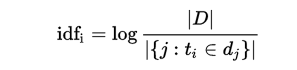
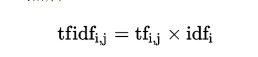
数据处理及应用
数据缩放
在特征工程中,除了算法使用代价函数,还可以将不同特征的量纲控制在一定范围内。
在梯度下降的使用中,面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯 度下降算法更快地收敛。面对不同量纲的数据,解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。以解决特征量纲的干扰。
算法表现为: \[ x_n = \frac{x_n-\mu}{s_n} \]
缺失值/离散值/极大极小值的处理
数据集难免存在缺失数据和录入错误的极端值数据,极大极小值也会影响模型,因此有不同的处理方式。
缺失值:判断数值的缺失是否合理。如果缺失不合理,考虑在数据足够大的条件下删除此数据;如果缺失合理或数据大小不适合删除此条数据,根据陈天奇大牛的建议,可以将此数据设为-999。 离散值:判断数值的离散是否合理,如果合理则保存此数据;如果不合理,则查看是否可以判断不合理原因给予修正;如无法修正,可以考虑作同缺失值的处理。 极大极小值:对不支持的模型,将其作为缺失值处理。
降维
数据集的某些无意义特征的存在不但降低模型计算速度,还会形成噪音影响模型。因此通过数据降维来提升模型质量。降维的计算比较复杂,在不同的模型中应用方式也各有不同,好在大型的机器学习库都提供了相应的算法,不多赘述,详见解析。
稀疏矩阵
稀疏矩阵是指将离散化的特征拆开,形成新的多个特征的一种手段,新生成的特征中只包含True(1)和False(0),且大部分元素都为False(0)的矩阵。实际上,连续性数据也可以通过分组达到此目的。
稀疏矩阵的目的主要是通过其自身的稀疏特性,通过压缩可以大大节省稀疏矩阵的内存代价,从而加快模型的运算速度,更重要的是当数据过大时,通过稀疏矩阵,标准化的算法将之前不可操作的数据变为可操作数据。
sklearn虽然集成了稀疏矩阵函数,但其效果并不优秀。在python语言中,可以依赖pandas的get_dummies函数将数据快速化为稀疏举证。具体信息详见:机器学习中的范数规则化之(一)L0、L1与L2范数。
调参
调参往往是模型碰到的最后敌人,当准备工作处理完毕后,不同的参数对结果会造成很大的不同,因此调参技巧是机器学习工程师必须要掌握的内容。直接贴一篇大神的文章,剩下的坑以后再补…
 ### 辛普森悖论 你是一位校长,假设有一天漂亮的秘书跑过来对你说:“校长,不好了,有很多男生在校门口抗议,他们说今年研究所女生录取率是男生的两倍,指责我们学校有性别歧视!” 这时你也很生气,说:“我不是特别交代,今年要尽量提升男生录取率以免落人口实吗?” 秘书赶紧回答说:“确实有交代下去,招生办说今年的男生确实比女生多,可是报告上显示男生所有学科录取率都比女生低了很多。” 那么问题是:有可能在男生所有学科录取率均比女生低的情况下,总性别比例还保持不变吗?
### 辛普森悖论 你是一位校长,假设有一天漂亮的秘书跑过来对你说:“校长,不好了,有很多男生在校门口抗议,他们说今年研究所女生录取率是男生的两倍,指责我们学校有性别歧视!” 这时你也很生气,说:“我不是特别交代,今年要尽量提升男生录取率以免落人口实吗?” 秘书赶紧回答说:“确实有交代下去,招生办说今年的男生确实比女生多,可是报告上显示男生所有学科录取率都比女生低了很多。” 那么问题是:有可能在男生所有学科录取率均比女生低的情况下,总性别比例还保持不变吗?